最小二乘法的简单应用

下面的例子用最小二乘法求解一个线性模型。
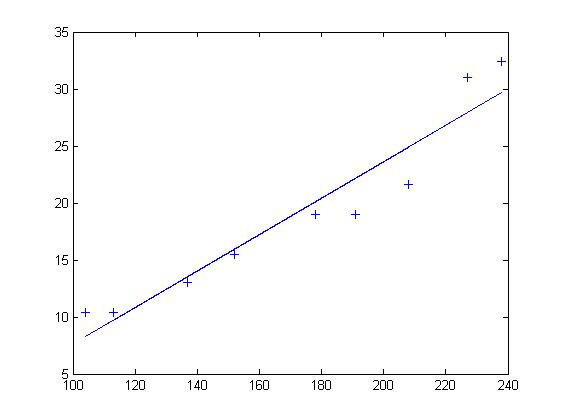
假设有10条船，分别测得它们的长度和宽度。以长度$L$（单位：米）为横轴，宽度$W$（单位：米）为纵轴，画出散点图如下：

由于散点近似落在一条直线上，尝试使用线性模型来描述长度和宽度之间的关系。
假设$W = k L + b$，其中$k$和$b$是线性模型的参数，是求解的具体对象。
定义损失函数$J(k, b) = \frac{1}{m} \sum_{i=1}^{m} (k L_i + b - W_i)^2$
用来衡量模型与实际的差距。其中$(L_i, W_i)$是第$i$个样本（观察对象）的长宽。
根据最小二乘法的定义，$k$和$b$的最优值通过优化目标函数得到：$\min_{k, b} J(k, b)$
由于目标函数是凸函数，局部最小值等同于全局最小值。对于连续可导函数，一个点是极值点的充要条件是在该点的一阶导数值为0。因此，令$\frac{\partial J}{\partial k} = \frac{2}{m} \sum_{i=1}^{m} (kL_i + b - W_i)L_i = 0$$\frac{\partial J}{\partial b} = \frac{2}{m} \sum_{i=1}^{m} (kL_i + b - W_i) = 0$
可以解得$b^{*} = \frac{1}{m} \sum_{i=1}^{m} (W_i - kL_i)$ $k^{*} = \frac{\sum_{i=1}^{m} L_i (W_i - b) }{\sum_{i=1}^{m} L_i^2}$
因此描述船的长度和宽度的关系的线性模型可以表示为$W = k^{*} L + b^{*}$

得到的直线如下图：